RUMUS ABC – Ada tiga cara yang bisa digunakan dalam memecahkan persamaan kuadrat, bisa dengan pemfaktoran, melengkapi bentuk rumus abc dan kuadrat. Pada artikel ini, kami akan tunjukan belajar cara ketiga, dengan menggunakan simple rumus abc.
Formula Abc atau yang bisa juga disebut rumus kuadrat, biasa dalam kegunaan pasti mengarah ke persamaan kuadrat yang sulit dikemukakan. Bahkan ada beberapa orang malah suka menggunakan metode ini sebagai cara ampuh mereka, tanpa dasar pemfaktoran atau mengisi bentuk kuadrat. Ini disebut formula abc karena komponen yang ada dalam formula cuma ada cara, a, b, dan c, yang tiap-tiapnya berupa koefisien x ², konstanta dan koefisien x.
Sebenarnya, formula ini berasal dari persamaan kuadrat umum yang dipecahkan dengan cara melengkapi bentuk kuadrat.
X1,2 = -b ± b2-4ac√2a
Untuk lebih jelasnya, mari masuk ke contoh pertanyaannya.
Rumus ABC

Penjelasan serta contoh soal:
Rumus ABC bisa kita anggap juga sebagai salah satu suatu rumus dalam menemukan akar-akar persamaan dari kuadrat. Ada beberapa syarat agar cara rumus bisa berfungsi.
Pertama bentuk persamaan kuadrat ini ke bentuk ax2 + bx + c = 0
Kedua nilai ≠ 0
Bilangan pada bawah tanda akar pastikan di rumus atas disebut dengan diskriminan (D), dimana D = b2-4ac
Rumus ABC juga dapat berlaku jika muncul pada nilai D> 0.
Persamaan Kuadrat

x² + 8x + 12 = 0, a = 1, b = 8, dan c = 12
x1,2=−b±b2–4ac√2a
x1,2=−8±82–4⋅1⋅12√2⋅1
x1,2=−8±64–48√2
x1,2=−8±16√2
x1,2=−8±42
x1,2=−4±2
x1=−4–2=−6
x2=−4+2=−2
Jadi, hasil himpunan samadengan adalah {-6, -2}.
Contoh Soal Kuadrat 2
x² + 3x – 10 = 0, a = 1, b = 3, c = -10
x1,2=−b±b2–4ac√2a
x1,2=−3±32–4⋅1⋅(−10)√2⋅1
x1,2=−3±49√2
x1,2=−3±72
x1=−3–72=−102=−5
x2=−3+72=42=2
Jadi, himpunan samadengan adalah {-5, 2}.
Contoh Soal Kuadrat 3
2x² + 4x – 6 = 0, a = 2, b = 4, c = -6
x1,2=−b±b2–4ac√2a
x1,2=−4±42–4⋅2⋅(−6)√2⋅2
x1,2=−4±64√4
x1,2=−4±84
x1,2=−1±2
x1=−1–2=−3
x2=−1+2=1
Jadi himpunan yang sudah selesai adalah {-3, 1}.
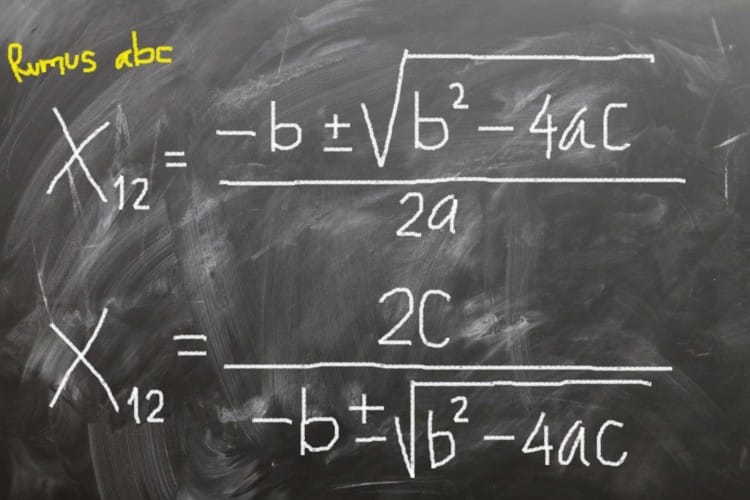
Demikian itu tadi adalah penjelasan singkat dari, rumus ABC, mengenai pembahasan rumus abc dalam penggunaan penyelesai persamaan kuadrat. Coba Anda bandingkan pada dua metode lainnya, jelas mana yang telah kita pelajari. Manakah metode yang mudah dan Anda suka. Semoga informasi ini bisa bermanfaat dan sampai jumpa lagi diartikel-artikel SatuJam.com lainnya.