RUMUS PHYTAGORAS – Dalam kehidupan sehari-hari manusia sering memanfaatkan teorema Phytagoras. Sala satu contoh pengaplikasian rumus Phytagoras adalah dalam bidang pertukangan. Ketika akan membangun sebuah rumah, seorang tukang biasanya akan mengukur lahan yang akan digunakan.
Hasil pengukuran tersebut kemudian digunakan untuk memastikan bahwa sudut-sudut bangunan rumah bentul-betul sudut siku-siku. Hal tersebut dapat dilakukan dengan cara menggunakan segitiga segitiga dengan ukuran sisi 60 cm, 80 cm, dan 100 cm.
Kemungkinan pak tukang sendiri juga tidak mengetahui alasan mengapa segitiga dengan ukuran seperti itu bisa membentuk sudut siku-siku. Agar kita bisa mengetahui bahwa cara yang digunakan pak tukang sudah benar atau belum, mari kita pelajari rumus Phytagoras.
Penemu Rumus Phytagoras

Rumus Phytgoras ditemukan oleh seorang ilmuwan yang berasal dari Yunani Selatan, yaitu Phytagoras pada tahun 582 – 496 sebelum masehi (SM). Salah satu penemuan Phytagoras yang paling terkenal dan populer hingga sekarang adalah teorema Phytagoras.
Pada teorema Phytagoras dinyatakan bahwa kuadrat sisi miring suatu segitiga siku- siku sama dengan jumlah kuadrat dari sisi-sisinya. Yang unik adalah kenaytaan bahwa sebenarnya rumus ini telah dikenal oleh orang Yunani 1.000 tahun sebelum masa Phytagoras.
Meskipun terdapat fakta bahwa rumus ini telah banyak dikenal orang sebelum kelahiran Phytagoras, akan tetapi teorema ini tetap dianggap temuan sebagai temuan Phytagoras. Hal ini dikarenakan ia merupakan orang pertama yang dapat membuktikan hal ini secara matematis dengan metode aljabar.
Menemukan Rumus Phytagoras
Berikut ini adalah cara untuk menemukan teorema Pythagoras. Dengan mengikuti kegiatan dibawah ini diharapkan Anda bisa mengetahui cara menemukan rumus Phytagoras.
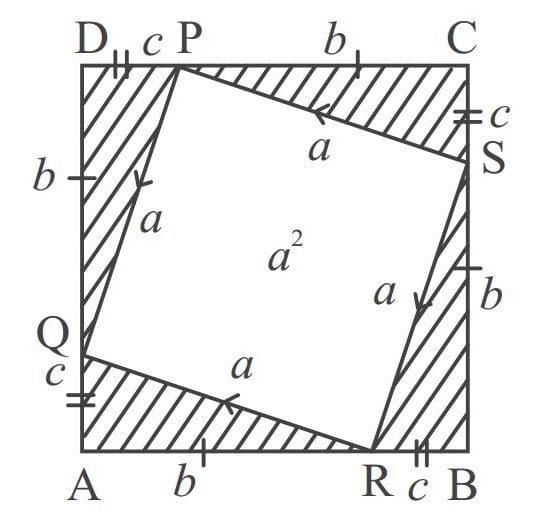
Pertama, siapkan dua potong kertas berbentuk persegi yang berukuran (b + c) cm seperti tampak pada Gambar i dan ii. Kita akan menemukan hubungan antara besarnya a, b, dan c.
Gambar i menunjukkan persegi ABCD berukuran (b + c) cm. Pada keempat sudutnya buatlah empat segitiga sikusiku dengan panjang sisi siku-sikunya b cm dan c cm.
Dari Gambar i tampak bahwa luas persegi ABCD sama dengan luas persegi (luas daerah yang tidak diarsir) ditambah luas empat segitiga siku-siku (luas daerah yang diarsir), sehingga diperoleh
luas daerah yang diarsir = luas empat segitiga siku-siku
dan
luas daerah yang tidak diarsir = luas persegi PQRS
= a x a = a2
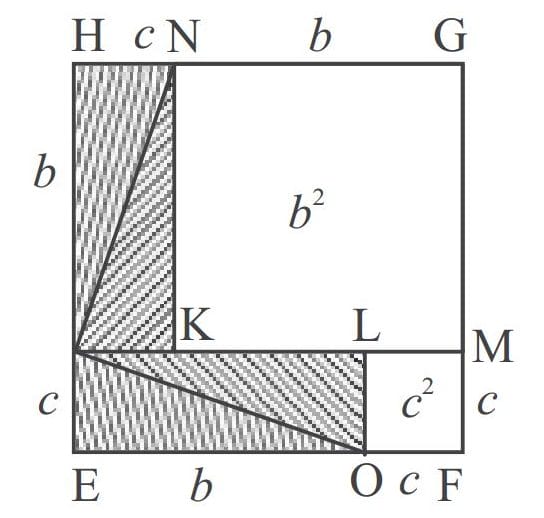
Lalu buatlah persegi EFGH berukuran (b + c) cm seperti tampak pada gambar ii. Pada dua buah sudutnya buatlah empat segitiga siku-siku sedemikian sehingga membentuk dua persegi panjang berukuran (b x c) cm.
Dari Gambar ii tampak bahwa luas persegi EFGH sama dengan luas persegi (luas daerah yang tidak diarsir) ditambah luas empat segitiga siku-siku (luas daerah yang diarsir), sehingga diperoleh,
luas daerah yang diarsir = luas dua persegi panjang
= 2 x b x c
= 2 bc
luas daerah yang tidak diarsir = luas persegi KMGN+ luas persegi OFML
= (b x b) + (c x c)
= b2 + c2
Dari Gambar i dan ii tampak bahwa ukuran persegi ABCD = ukuran persegi EFGH, sehingga diperoleh
luas persegi ABCD = luas persegi EFGH
2bc + a2 = 2bc + b2 + c2
a2 = b2 + c2
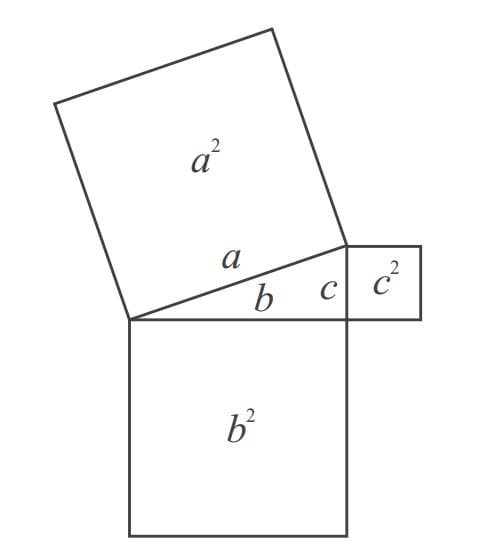
Kesimpulan di atas jika digambarkan akan tampak seperti pada Gambar iii.
Luas daerah persegi yang panjang sisinya adalah sisi miring suatu segitiga siku-siku sama dengan jumlah luas daerah persegi yang panjang sisinya adalah sisi siku-siku segitiga tersebut.
Kesimpulan tersebut selanjutnya dikenal dengan teorema Pythagoras. Teorema Pythagoras tersebut selanjutnya dapat dirumuskan seperti berikut.
Untuk setiap segitiga siku-siku, berlaku kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi siku-sikunya.
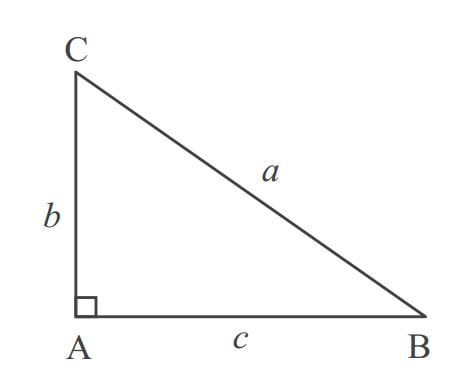
Jika ABC adalah segitiga siku-siku dengan a panjang sisi miring, sedangkan b dan c panjang sisi siku-sikunya maka berlaku
a2 = b2 + c2.
Pernyataan di atas jika diubah ke bentuk pengurangan menjadi
b2 = a2 – c2
atau
c2 = a2 – b2
Demikian artikel mengenai rumus Phytagoras yang membahas penemu dan cara menemukan rumus Phytagoras. Semoga bisa bermanfaat bagi Anda agar bisa memahami lebih baik lagi rumus Phytagoras. Salam 🙂